
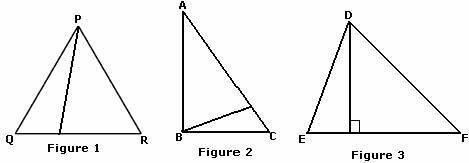
The orthic triangle of an acute triangle gives a triangular light route. The sides of the orthic triangle are parallel to the tangents to the circumcircle at the original triangle's vertices. This is the solution to Fagnano's problem, posed in 1775. In any acute triangle, the inscribed triangle with the smallest perimeter is the orthic triangle. The extended sides of the orthic triangle meet the opposite extended sides of its reference triangle at three collinear points. Let A, B, C denote the vertices and also the angles of the triangle, and let a = | B C ¯ |, b = | C A ¯ |, c = | A B ¯ | If one angle is a right angle, the orthocenter coincides with the vertex at the right angle. The orthocenter lies inside the triangle if and only if the triangle is acute. In geometry, the altitude is a line that passes through two very specific points on a triangle: a vertex, or corner of a triangle, and its opposite side at a. The three (possibly extended) altitudes intersect in a single point, called the orthocenter of the triangle, usually denoted by H. Three altitudes intersecting at the orthocenter It is common to mark the altitude with the letter h (as in height), often subscripted with the name of the side the altitude is drawn to. Also the altitude having the incongruent side as its base will be the angle bisector of the vertex angle. In an isosceles triangle (a triangle with two congruent sides), the altitude having the incongruent side as its base will have the midpoint of that side as its foot. The altitudes are also related to the sides of the triangle through the trigonometric functions. Thus, the longest altitude is perpendicular to the shortest side of the triangle. It is a special case of orthogonal projection.Īltitudes can be used in the computation of the area of a triangle: one-half of the product of an altitude's length and its base's length equals the triangle's area. The process of drawing the altitude from the vertex to the foot is known as dropping the altitude at that vertex. The length of the altitude, often simply called "the altitude", is the distance between the extended base and the vertex. The intersection of the extended base and the altitude is called the foot of the altitude. An interesting fact is that the three altitudes always pass through a common point called the orthocenter of the triangle. This line containing the opposite side is called the extended base of the altitude. An altitude is a line which passes through a vertex of a triangle, and meets the opposite side at right angles. In geometry, an altitude of a triangle is a line segment through a vertex and perpendicular to (i.e., forming a right angle with) a line containing the base (the side opposite the vertex). The complement of this angle is the zenith angle (z), that is defined by the vertical and the line to the Sun (i.e., the angle of incidence of beam radiation. The three altitudes of a triangle intersect at the orthocenter, which for an acute triangle is inside the triangle.


 0 kommentar(er)
0 kommentar(er)
